🌟 TL;DR:多智能体的美好愿景与残酷现实
1986年,图灵奖得主Fred Brooks在软件工程领域提出了著名的”没有银弹”理论:没有任何一种技术或方法能够独自带来软件工程生产力的数量级提升。近四十年后,这个深刻洞察在AI领域再次得到验证——你是否也曾经历过这样的挫折:

图片来自百度百科
💭 花费大量时间精心设计多智能体系统,期待着”1+1>2″的效果,结果却发现性能提升微乎其微,甚至还不如单个模型?
最近一项来自南佛罗里达大学和罗格斯大学的研究揭示了这个问题的根源,并提出了一个名为Know-The-Ropes(KtR)了解门道的解决框架。研究者们通过严格的实验证明,简单地堆叠更多智能体并不能带来预期的性能提升,真正的突破需要基于领域知识的系统性分解。

🎯 NFL:为什么没有万能的Agent架构
无免费午餐定理(No Free Lunch Theorem,NFL)由David H. Wolpert和William G. Macready于1997年提出,其核心观点极其简洁却影响深远:

图片来自百度百科
📊 对于所有可能的优化问题,任何两个优化算法的平均性能都是相同的。
这意味着如果算法A在某些问题上表现优于算法B,那么必然存在其他问题使得算法B优于算法A。对于多智能体系统设计而言,这个定理告诉我们追求”万能提示模板”或”通用架构”注定是徒劳的——真正有效的解决方案必须深度结合具体问题的特性和约束条件,利用领域知识来打破”平均性能相等”的魔咒。
💡 这正是KtR框架强调基于领域先验进行系统性分解的理论依据:没有银弹,只有针对特定问题域的最优解决方案。
⚠️ 当前多智能体系统的三大痛点
🔴 痛点一:不当分解导致的系统性混乱
你可能遇到过这样的情况:将一个复杂任务随意分配给多个智能体,结果发现智能体之间职责重叠、边界模糊,甚至相互冲突。
根本原因:
- ❌ 缺乏系统性分解方法
- ❌ 仅凭直觉进行任务划分
- ❌ 未考虑任务间的逻辑依赖关系和数据流向
后果:不仅无法提升性能,反而会引入额外的协调成本和错误传播风险。
🔴 痛点二:验证开销的二次增长陷阱
随着智能体数量的增加,系统的验证成本呈现二次增长趋势,这是许多开发者始料未及的。
关键发现:
- 📈 每增加一轮对话,延迟和成本几乎呈指数级增长
- 🔍 传统验证方法要么依赖脆弱的思维链启发式,要么消耗大量token预算
- ⚡ 当任务需要超过2-3轮协调时,多智能体系统的性能提升往往变成负数
🔴 痛点三:提示过拟合与评估泄漏
这是一个容易被忽视但影响深远的问题:
现象:许多多智能体框架在特定数据集上表现出色,但一旦移除评估泄漏和提示过拟合,性能提升就会急剧下降到个位数百分比。
根源:
- 🎯 过度依赖手工调优的提示词
- 🏗️ 没有建立起系统性的设计原则
- 🔄 面对新问题域时,精心调优的提示往往失效
🛠️ KtR:用算法思维设计Multi-Agent
💡 核心理念:将领域先验转化为算法蓝图
KtR框架的核心思想是将已知的、有效的算法程序转换为连贯的多智能体架构。
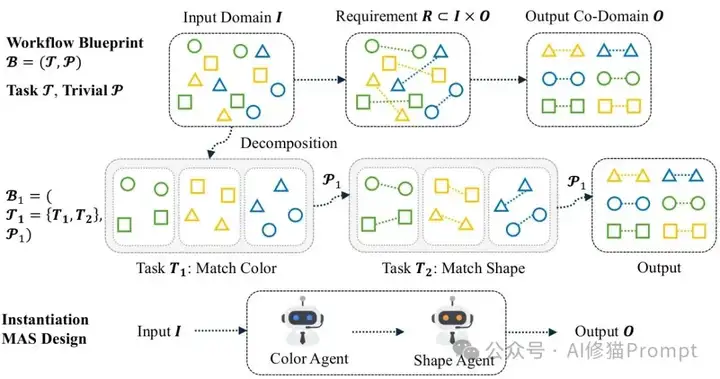
KtR框架示意图
📐 六个核心定义:构建严谨的形式化框架
KtR框架通过六个精确的数学定义建立了完整的理论基础:
- 良好形式化任务:包含输入域、输出共域和需求关系三个要素
- 工作流蓝图:定义了任务集合和编排协议
- 分解过程:规定了如何将复杂任务递归分解为更简单的子任务
- 可处理性:判断任务是否在模型能力范围内
- 可处理层次结构:确保每个叶子任务都能被可靠解决
- 系统实例化:将蓝图转化为具体的多智能体系统
🔄 三步实施流程:从理论到实践的桥梁

- 步骤一:定义初始蓝图,将原始任务包装成标准格式
- 步骤二:在领域启发式指导下构建可处理层次结构,递归分解直到每个叶子任务都在基础模型的能力范围内
- 步骤三:将终端蓝图实例化为具体的多智能体系统
🔑 关键:每个子任务必须能够被现有模型通过零样本或轻量增强(如思维链、微调、自检)可靠地解决。
🎒 背包问题:小模型如何实现大突破
🎯 问题设定:经典NP难题的挑战
背包问题是计算机科学中的经典优化问题:
📦 给定N个物品(每个有重量和价值)和一个容量限制,目标是选择物品子集使总价值最大且总重量不超过容量。
为什么选择这个问题:
- ✅ 有成熟的动态规划解决方案
- ✅ 足够复杂以测试框架的有效性
- ✅ 故意选择轻量级的GPT-4o-mini作为基础模型,证明KtR能让小模型实现大突破
🤖 三智能体分工:动态规划的精确映射
KtR将经典的动态规划算法精确地映射到三个专门智能体上:

🚀 瓶颈识别与精准优化:从18%到95%

KSP性能对比图
发现瓶颈:
通过系统性的性能分析,研究者发现修剪智能体是整个系统的瓶颈,其准确率随着可行状态数量增加而急剧下降。
精准优化:
仅对修剪智能体进行了轻量级微调(使用1200个训练样例),就将整个系统的准确率从不足18%提升到95%!
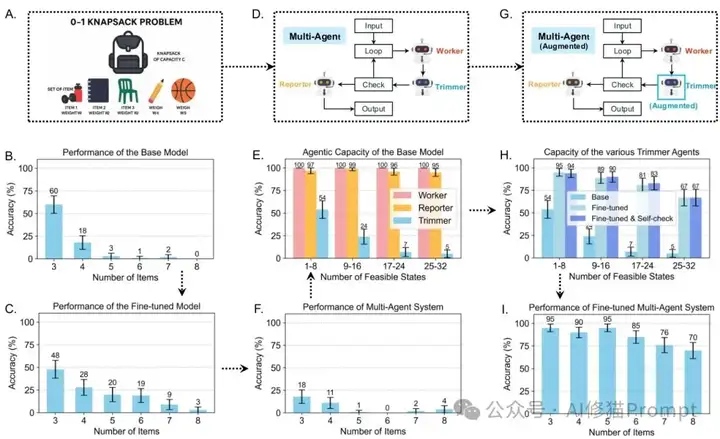
KSP详细评估结果
💥 震撼结果:通过精确的瓶颈识别和有针对性的优化,一个由小模型组成的多智能体系统竟然能够达到如此高的性能水平。
🎯 任务分配问题:可扩展性的有力证明
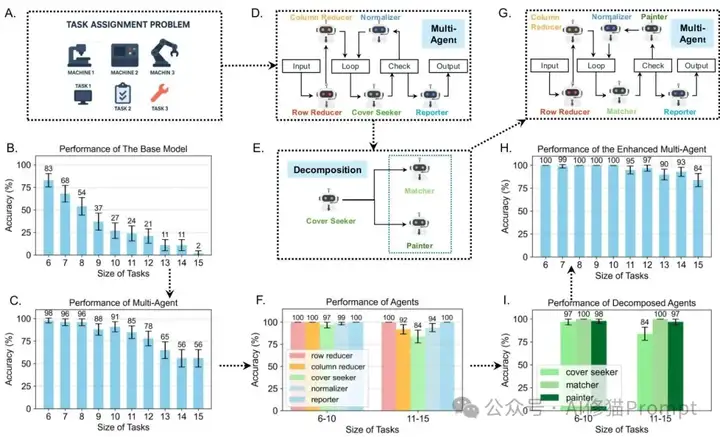
📚 匈牙利算法简介
任务分配问题是运筹学中的经典优化问题:
👥 给定n个工人和n个任务,每个工人完成每个任务都有特定的成本,目标是找到一个一对一的分配方案使总成本最小。
匈牙利算法由Harold Kuhn在1955年提出,是解决这类问题的经典多项式时间算法。
算法核心步骤:
- 🔢 矩阵行列约简
- 🔍 寻找零元素覆盖
- ➕ 创建新零元素
- 🔄 迭代直到找到最优解
实际应用:生产调度、资源分配、物流配送等场景
🤖 匈牙利算法的六智能体实现
为了证明KtR框架的可扩展性,研究者使用更强的o3-mini模型,将匈牙利算法分解为六个智能体:
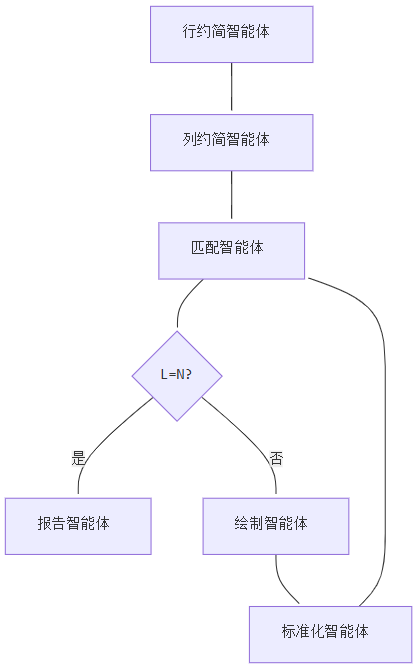
TAP性能对比图
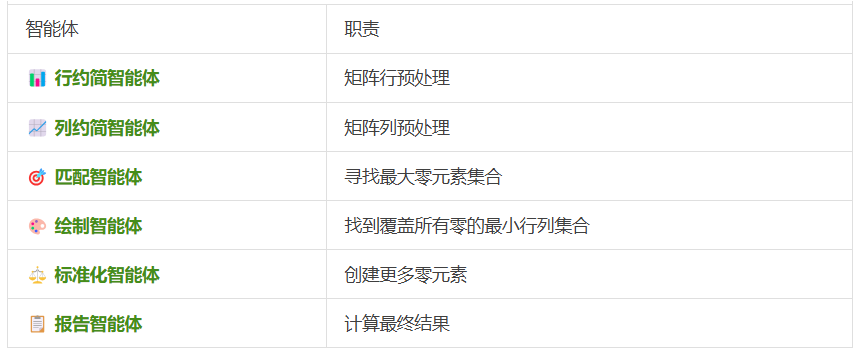
🎊 进一步分解的威力:从84%到100%的完美表现
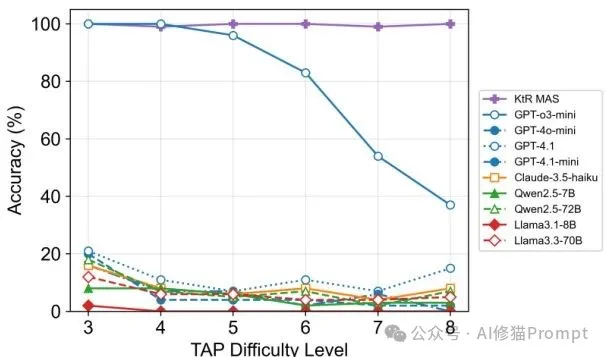
发现新瓶颈:
在初始设计中,研究者发现覆盖寻找任务成为新的瓶颈。
递归分解:
将其进一步分解为匹配和绘制两个子任务。
TAP详细评估结果
结果:
- 🎯 问题规模6-10:达到近乎完美的100%准确率
- 📈 更大规模问题:保持84%以上的高性能
✨ 核心优势:通过系统性的分解和有针对性的优化,可以让多智能体系统的性能随着基础模型能力的提升而同步增长。
💻 实现细节:从理论到代码的完整路径
📝 提示词工程:精确规范胜过花哨技巧
KtR框架的提示词设计遵循“精确规范胜过花哨技巧”的原则:
设计要素:
- ✅ 明确的输入输出格式定义
- ✅ 具体的处理步骤说明
- ✅ 严格的返回格式要求
- ✅ 避免模糊表述可能带来的歧义
成功关键:这种精确的规范化设计确保了智能体行为的可预测性和系统的稳定性。
🔄 消息传递与错误处理:工程化的系统设计
KtR框架采用了成熟的软件工程实践:
核心组件:
- 📡 消息总线:智能体间数据传递,支持异步处理和消息队列管理
- 🛡️ 错误处理机制:重试逻辑、降级策略和备用方案
- 🔒 故障隔离:确保单个智能体的失败不会导致整个系统崩溃
📊 性能监控与瓶颈识别:数据驱动的优化策略
监控指标:
- 🎯 准确率
- ⏱️ 响应时间
- 💾 资源消耗
优化策略:
- 🔧 微调
- 🔍 自检
- 📝 提示优化
- 🔄 进一步分解
🏪 实战案例:RFM客户分析系统的KtR实现
为了验证KtR框架在实际业务场景中的效果,我基于论文理论实现了一个完整的RFM客户分析系统。
🤖 智能体分工设计
确定性智能体(5个):
- 📊 DataPreprocessor:数据预处理
- 📅 RecencyCalculator:最近性计算
- 🔢 FrequencyCalculator:频率计算
- 💰 MonetaryCalculator:货币价值计算
- 📈 RFMScoring:RFM评分
LLM智能体(3个):
- 🎯 CustomerSegmentation:客户分群
- 🧠 BusinessInsight:商业洞察
- 📋 ReportGenerator:报告生成
🔧 核心技术特点
- 🏗️ 混合架构:数学计算使用确定性算法,智能分析使用LLM
- 📦 增强的JSON解析:多策略提取、平衡括号匹配、常见错误修复
- ⚡ 批处理策略:小批量处理(8个客户/批次)确保LLM稳定性
- 💬 自然语言fallback:当JSON格式限制过严时,允许LLM生成自然语言再解析
🛍️ 业务场景适配
系统以”某爽肤水专营店”为例,模拟真实电商场景下的客户分析需求。通过行业特定的业务上下文配置,系统能够生成符合护肤品行业特点的客户分群策略和营销建议。
🎉 运行效果展示
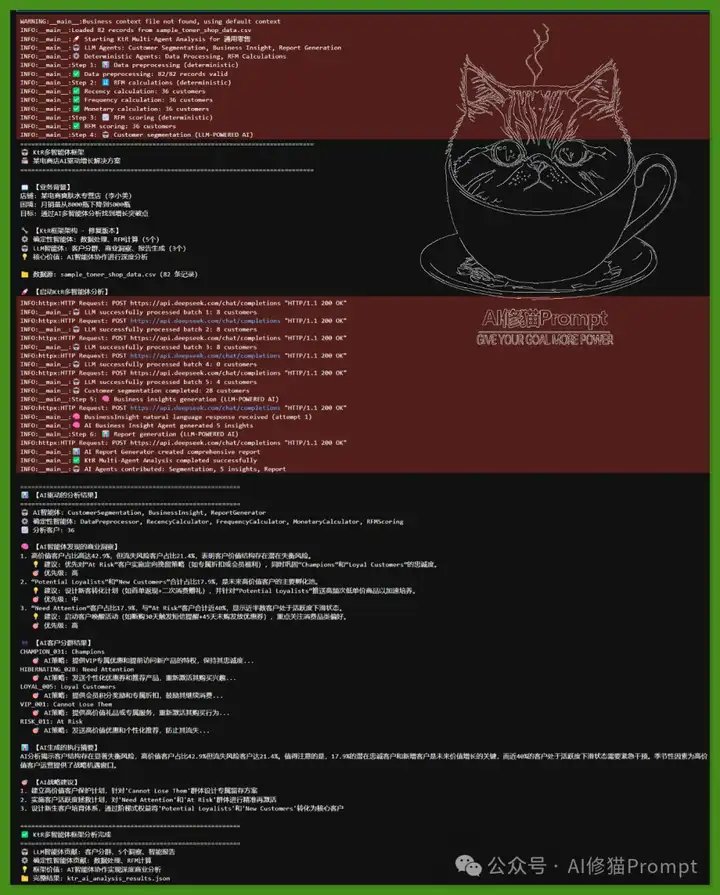
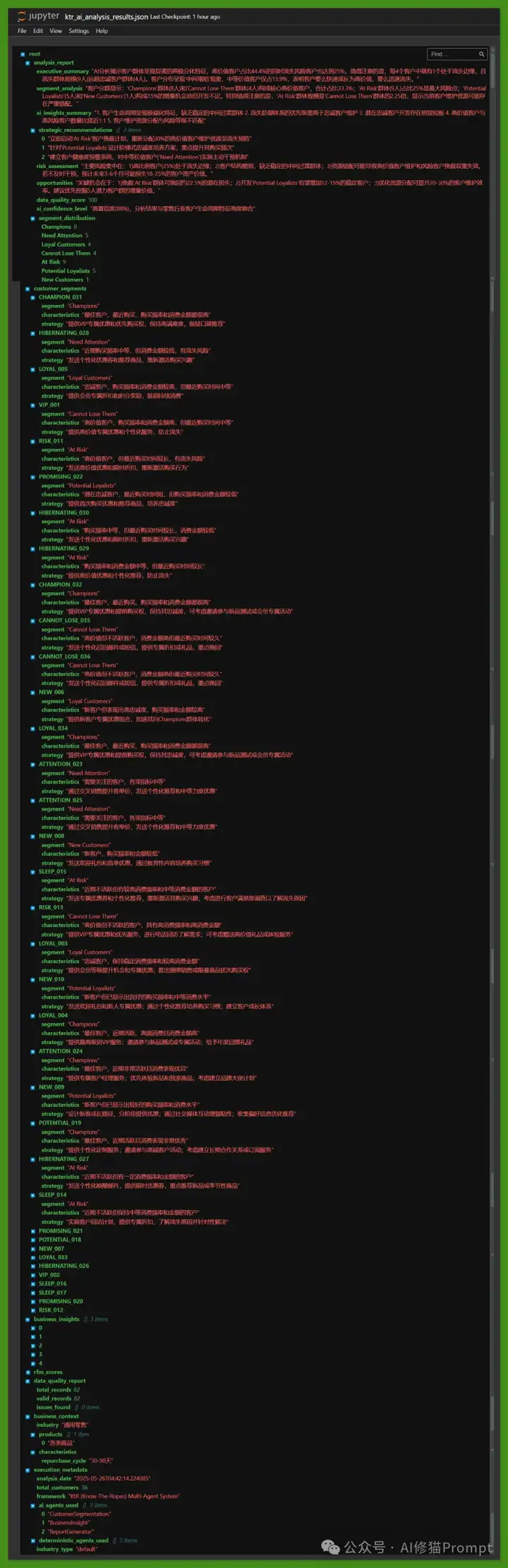
成功验证:
- 🤖 LLM智能体真正参与核心分析:客户分群5个批次全部成功,商业洞察生成5个深度发现,报告生成完整专业
- ⚙️ 确定性智能体处理基础计算:数据预处理、RFM计算等数学操作使用算法实现
- 💡 系统价值清晰可见:最终输出明确标识”LLM智能体贡献:客户分群、5个洞察、智能报告”
🏆 重要证明:KtR框架不仅在理论上具有说服力,在实际应用中也能够产生真正的商业价值。通过有纪律的分解和精确的智能体设计,小模型也能够在复杂业务场景中发挥出色的分析能力。
🎯 适用场景:KtR框架的实际应用价值
📊 结构化优化问题:天然的适用领域
KtR框架特别适合那些有明确数学表述和成熟算法解决方案的结构化优化问题:
应用领域:
- 🚚 供应链优化:库存管理和路径规划
- 💼 金融领域:投资组合配置和风险管理
- 🏭 制造业:生产调度和资源分配
核心价值:将算法转化为可扩展的多智能体系统,既保持了算法的理论保证,又获得了分布式处理的灵活性。
🔄 多步骤决策流程:复杂业务逻辑的理想选择
对于需要多个步骤、有明确依赖关系的复杂决策流程:
典型场景:
- 🏥 医疗诊断:症状分析→检查建议→诊断推理→治疗方案
- ⚖️ 法律案件分析:事实梳理→法条匹配→证据评估→判决建议
- 🏗️ 工程设计:需求分析→方案设计→可行性评估→优化改进
关键要求:每个步骤都有明确的输入输出规范和质量标准,便于验证和优化。
🎓 领域专业化任务:专业知识的系统化应用
KtR框架在需要深度领域知识的专业化任务中展现出独特优势:
应用场景:
- 🔬 科学研究辅助:文献综述、实验设计、数据分析、结论验证
- 📚 教育内容生成:课程设计、习题生成、评估标准、个性化辅导
- 💻 技术文档处理:需求分析、架构设计、代码生成、测试验证
共同特点:有明确的专业标准和成熟的方法论,KtR框架能够将这些专业知识系统化地嵌入到多智能体协作中。
⚠️ 局限性与挑战:诚实面对现实约束
🎓 领域知识依赖:专业门槛的双刃剑
最大优势 = 主要限制:对领域知识的强依赖性
挑战:
- 📚 需要深入理解目标问题域的算法和方法论
- 👥 要求开发者具备相当的专业背景,或与领域专家密切合作
- 🚪 提高了应用难度
价值:确保了系统设计的科学性和可靠性
🌐 开放域推理的未知领域
当前验证范围:主要在结构化的优化问题上得到验证
未知领域:
- 🤔 开放域推理
- 🎨 创意生成
- 🖼️ 多模态理解
现实定位:KtR框架更适合作为专门模块的设计方法,而不是整个系统的架构基础。
🤖 自动化程度的提升空间
当前状态:仍然需要大量的人工设计和调优工作
需要人工参与的环节:
- 🔧 任务分解
- 🔍 瓶颈识别
- 📝 提示词编写
- 📊 性能优化
未来方向:
- 🤖 自动化瓶颈识别
- 🧠 智能化任务分解
- 🔄 端到端的系统优化
🎯 究竟该如何设计多智能体系统
KtR框架的真正价值不仅在于其具体的技术实现,更在于它重新定义了多智能体系统的设计哲学。
💡 核心启示
它告诉我们:
- ✅ 真正有效的多智能体系统不是简单的模型堆叠,而是基于深度领域知识的系统工程
- ✅ 无免费午餐定理在AI系统设计中具有重要指导意义:没有万能的架构,只有针对特定问题的最优解决方案
🛠️ 实践指导
对于正在开发Agent产品的你来说,KtR框架提供了一个全新的思路:

🌟 可能的方向
🚀 真正的突破不是来自于更大的模型或更多的计算资源,而是来自于更深入的问题理解和更科学的系统设计,从而形成可交付结果的闭环。
这或许就是下一代AI系统的核心竞争力所在。
📝 本文基于论文《Know the Ropes: A Heuristic Strategy for LLM-based Multi-Agent System Design》https://arxiv.org/pdf/2505.16979 的深度解读和实践验证